Functional programming is a programming paradigm, which allows us to write our programs in a declarative and composable way by combining functions.

Functional programming in TypeScript?

Functional programming is language agnostic, meaning that we can apply it using almost any language. The only requirement is that the language treats functions as first-class citizens, which means that we can:

• Assign functions to variables.
• Pass functions as arguments to other functions.
• Use functions as return values from other functions.

All of the above is doable in TypeScript, which makes it a suitable choice to write code in the FP paradigm.

There are several libraries such as ramda or fp-ts, that include features to allow us to write in a more pure functional style. In this series of articles, we won’t be using any of these, just vanilla TS.

But what is Functional Programming about?

FP is about taking some input, and process it by using a chain of transformations (each transformations is accomplished by a function). When each of these functions is called with some given arguments, it will always return the same result (pure function).

In constrast, an impure function, like the ones we use in imperative programming, can have side effects (such as modifying the program’s state or taking input from a user). Side effects are considered undesirable in pure functional programming because they make functions less predictable and harder to test.

Some defining features of FP are:

• Functions are at the center of the paradigm. We end up with a bunch of reusable units of code, which leads to having to write less code to achive the same results.
• These functions are quite deterministic, meaning, given a given input, they always return the same output, regardless of the program’s state.
• Easy to test code: As a result, when writing tests for the functions, we don’t have to worry about program’s state.
• Easier to debug: FP aims to minimize or isolate side effects to make code more predictable, testable, and easier to debug.
• We’ll see that for or while loops are not used in FP; in these scenarios we use recursion.

As with any other approach, it will take time to become comfortable using it. As a result, noticing its benefits will take some time.

Pure Functions

A pure function has the following characteristics:

• It’s deterministic, meaning that given the same input (given in the arguments), the function always returns the same output. That implies that the function shouldn’t be affected by the state of the program (no side causes), only by its input.
• A pure function has no side effects, meaning that calling such a function should not mutate the state of the program.

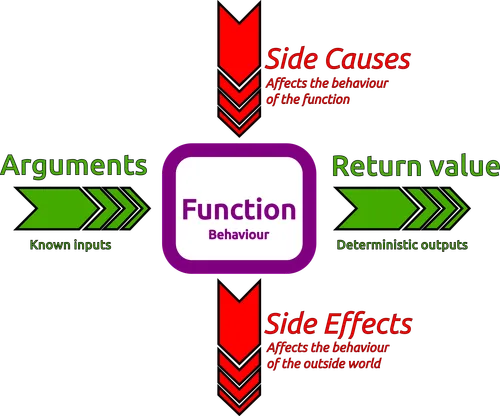
In FP, we don’t use variables only constants. Each transformation (function call) returns a new value, which is assigned to a constant. This constant can be used as input (argument) in the next transformation.

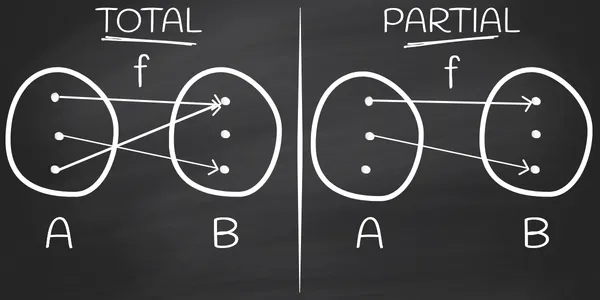
Total vs Partial Functions

A total function is a function that is defined for all possible inputs in its domain. This means that for every input value in the domain, the function will produce a valid output. For example:

function add(a: number, b: number): number {
  return a + b
}

A partial function is a function that is defined for only a subset of inputs in its domain. For some inputs, the function may not produce a valid output or may result in an error. For example:

function divide(a: number, b: number): number {
  if (b === 0) {
    throw new Error('Division by zero is not allowed')
  }
  return a / b
}

So the main difference is that total functions map all of its inputs to some output value, whereas partial functions map only a subset of its inputs to some output:

Key Differences Between Total and Partial Functions

Why Total Functions Are Preferred in Functional Programming

1. Predictability: Total functions are easier to reason about because they are guaranteed to work for all inputs.

2. No Runtime Errors: Total functions eliminate the risk of runtime errors caused by invalid inputs.

3. Composability: Total functions can be composed more easily because they always produce valid outputs, which can be passed as inputs to other functions.

4. Immutability: Total functions align with the principles of functional programming, where functions are deterministic and side-effect-free.

How to Handle Partial Functions in FP

In functional programming, partial functions are often avoided or handled explicitly using techniques like:

1. Option Types (e.g., Maybe or Option): Wrap the result in a type that explicitly represents the possibility of failure. For example:

function safeDivide(a: number, b: number): number | null {
  return b === 0 ? null : a / b
}

2. Validation: Validate inputs before calling the function to ensure they are within the valid subset.

function divide(a: number, b: number): number {
  if (b === 0) {
    throw new Error('Division by zero is not allowed')
  }
  return a / b
}

Function Composition

Most of what we do in FP is composing functions, which consists in combining two or more functions to produce a new function; The output of one function becomes the input of the next one. Function composition allows us to build complex operations by combining smaller, reusable functions.

For example, imagine we have the function increment:

type Increment = (x: number) => number

const increment = (x: number): number => x + 1

And also the function stringify:

type Stringify = (x: number) => string

const stringify: Stringify = (x) => x.toString()

Using function composition we can define a higher-order function named incrementAndStringify, where we connect the output tof increment to the input of stringify:

type IncrementAndStringify = (x: number) => string
const incrementAndStringify: IncrementAndStringify = (x) => stringify(increment(x))

const result: string = incrementAndStringify(1)
console.log(result) // "2"

const stringify = (x: number): string => x.toString()

const add = (a: number, b: number): number => a + b

const result = stringify(add(2, 3))
const result2 = stringify(5) // We can replace add(2, 3) with 5

A Step Up

In the previous section, we were composing functions by hardcoding their names into the composed version. It would be nicer if we could create a third function, which takes two functions, and return their composition:

type Increment = (x: number) => number
const increment: Increment = (x) => x + 1

type Stringify = (x: number) => string
const stringify: Stringify = (x) => x.toString()

type Compose = (
    f: (x: number) => string,
    g: (x: number) => number
) => (x: number) => string

const compose: Compose = (f, g) => x =>  f(g(x))

const incrementAndStringify = compose(stringify, increment)
console.log(incrementAndStringify(33)) // "34"

Adding Generic Types

It would be even nicer, if we could define our compose function so that it’s not limited to the types string and number. Check this out:

type Increment = (x: number) => number
const increment: Increment = (x) => x + 1

type Stringify = (x: number) => string
const stringify: Stringify = (x) => x.toString()

type IncrementAndStringify = (x: number) => string

type Compose = <T, U>(
    f: (x: T) => U,
    g: (x: T) => T
) => (x: T) => U

const compose: Compose = (f, g) => x =>  f(g(x))

const incrementAndStringify: IncrementAndStringify = compose(stringify, increment)
console.log(incrementAndStringify(41)) // "42"

In the code above we are using two generics that allow us to replace T and U by any types. That way we can compose any two functions with different type signatures. In the way we defined the compose function above, we have only two constraints:

• The type of input of g, f, and our compose function is the same.
• The type of output of f and our compose function is the same.

Using function composition allows us to reuse a lot of small functions by composing them in different ways, to achieve different results. Testing each of these functions is easy.

A Generic compose Function

We could take it a step further, and define a super generic compose function, that could take any two functions, no matter their signature:

type Compose = <A, B, C>(
  f: (x: B) => C,
  g: (x: A) => B
) => (x: A) => C

const compose: Compose = (f, g) => x =>  f(g(x))

const incrementAndStringify: IncrementAndStringify = compose(stringify, increment)
console.log(incrementAndStringify(41)) // "42"

Here, we define a generic compose function compose with three generic types:

• A: The type of input to g (the first function in the composition), and to the compose function itself.
• B: The type of input to f, and the output from g.
• C: The type of output from f, and the output of compose (the final result).

React Router is a multi-strategy router for React, which means it can be used in different ways depending on the needs of your application. In this guide, we’ll explore the framework mode, which is a new way to use React Router that allows you to define your routes in a more declarative way.

Generating a new React project

The framework mode is the one that offers the most features (check comparison table), hence it has a few dependencies than the other modes. For that reason, setting it up manually it’s a bit tricky. A better idea is to generate a new project using the following command:

npx create-react-router@latest my-react-router-app

Where my-react-router-app is the name of our project. This command will generate a new React project with the all the necessary dependencies to use React Router in framework mode.

Once we have our project created, we can navigate to the root folder and start the development server:

cd my-react-router-app
npm run dev

Important Files

If we open the project in our code editor, we should see a bunch of files and folders, but the most important ones are inside the app folder:

• app/root.tsx: This is the entry point of our application, from where we export:
  • The Route.LinksFunction.
  • The Layout component.
  • The App component.
  • An ErrorBoundary component.
• app/routes.ts: This is where we define our routes.

Defining Routes

Routes must be defined in the app/routes.ts file. For example, let’s define a simple route that renders a route module named home.tsx when the URL is /:

import { type RouteConfig, index } from '@react-router/dev/routes'

export default [
    route('/', 'routes/home.tsx')
] satisfies RouteConfig

The route function is known as a route matcher; this route matcher takes two arguments:

• A URL pattern to match the URL, in this case ’/’.
• A file path to the route module that will be rendered when the URL matches the pattern.

Since having a route for the home page is a common use case, React Router provides a helper function called index that does the same as route('/', 'routes/home.tsx'):

import { type RouteConfig, index } from '@react-router/dev/routes'

export default [
    route('/', 'routes/home.tsx')
    index('routes/home.tsx')
] satisfies RouteConfig

These are the contents of routes/home.tsx:

export default function Index() {
  return <h1>You are at Index</h1>
}

You made a GET request to / but did not provide a `loader` for route "routes/home", so there is no way to handle the request.

Adding a Loader

Let’s define data loading for our route module. There are two ways to do this:

• Client Data Loading, using the clientLoader function.
• Server Data Loading, using the loader function.

Client Data Loading

Let’s add a clientLoader function to fetch a list of TODOs from the JSONPlaceholder API. We’ll render the list of TODOs in the home.tsx route module:

import type { Route } from '../+types/root'

interface Todo {
  userId: number
  id: number
  title: string
  completed: boolean
} // Better move this type to a separate file (types/todo.ts) and import it here.

export async function clientLoader() {
  const response = await fetch('https://jsonplaceholder.typicode.com/todos')
  if (!response.ok) {
    throw new Error('Failed to fetch todos')
  }

  return response.json()
}

export default function Home({ loaderData }: Route.ComponentProps) {
  return (
    <main>
      <h1>You are at Index</h1>
      <h2>Todos</h2>
      <ul>
        {(loaderData ?? []).map((todo: Todo) => (
          <li key={todo.id} className="py-4">
            <h3>{todo.title}</h3>
            <p>{todo.completed ? 'Completed' : 'Not Completed'}</p>
          </li>
        ))}
      </ul>
    </main>
  )
}

Yeah, I know, it’s a lot of code for rendering just a TODO list!, but let’s break it down:

• We define a Todo type that represents the structure of the data we’re going to fetch.
• Note that clientLoader runs on the client side, like a traditional SPA; open the network tab to verify the request.
• In the React component, we destructure the loaderData prop to access the data fetched by the clientLoader function. Then we render the list of TODOs.

// HydrateFallback is rendered while the client loader is running
export function HydrateFallback() {
  return <div>Loading...</div>;
}

Server Data Loading

Server Data Loading works the same way as the clientLoader, but it runs on the server side. Let’s add a loader function to fetch the individual TODOs:

import type { Route } from '../+types/root'
import { Link } from 'react-router'
import type { Todo } from 'types/todo'

export async function loader({ params }: { params: { id: string } }) {
  const { id } = params
  const response = await fetch(`https://jsonplaceholder.typicode.com/todos/${id}`)
  if (!response.ok) {
    throw new Error('Failed to fetch todos!')
  }

  return await response.json()
}

export default function Todo({ loaderData }: Route.ComponentProps) {
  const todo = loaderData ? (loaderData as Todo) : null

  return (
    <main>
      <Link to="/">Back Home</Link>

      {todo && (
        <div key={todo.id}>
          <h3>{todo.title}</h3>

          <p>{todo.completed ? 'Completed' : 'Not Completed'}</p>
        </div>
      )}
    </main>
  )
}

The loader function runs on the server, so you won’t be able to see the network request in the browser’s console. We get good old HTML from the backend, which you can verify it by disabling JavaScript in the browser.

import { type RouteConfig, index, route } from '@react-router/dev/routes'

export default [
    index('routes/home.tsx'),
    route('todo/:id', 'routes/todo.tsx')
] satisfies RouteConfig

Adding a Layout Route

It’s pretty common to have a layout component shared amongst several routes in our application. As you can see, both our route modules have a main element repeated (in real life scenarios we’d have way more than that). We can define a layout route in the app/root.tsx file:

import { Layout } from '@react-router/dev/routes'

export default [
    layout("./components/layout.tsx", [
        index('routes/home.tsx'),
        route('todo/:id', 'routes/todo.tsx')
    ]),
]

An this is the content of components/layout.tsx:

import { Outlet } from 'react-router'

export default function Layout() {
  return (
    <div>
      <header>
        <h1>TODO list app</h1>
      </header>

      <main>
        <Outlet />
      </main>
    </div>
  )
}

So the way this works is that the Layout component is rendered for all the nested routes, wrapping them, and the Outlet component is used to render the child routes.

Nested routes

We can also define nested routes in our application. Let’s say we want to have a

Adding a 404 Route

This one is really simple, we just have to add a route matcher that matches any URL:

import { type RouteConfig, index, route } from '@react-router/dev/routes'

export default [
    index('routes/home.tsx'),
    route('todo/:id', 'routes/todo.tsx'),
    route('*', 'routes/not-found.tsx')
] satisfies RouteConfig

And the content of routes/not-found.tsx:

export default function NotFound() {
  return <h1>404 - Not Found</h1>
}

uv is an extremely fast package and project manager for Python, written in Rust. I hear you mumbling, another package manager for Python? Bro, this time is different, hear me out, uv really is the future. In this post we’ll spend some minutes learning how to use it.

What can I do with it?

Lots of things, but from the top of my head:

• Install packages, duh, but 10-100x faster than pip, the official package manager for Python.
• Install and manage Python versions; goodbye pyenv.
• It’s also a project manager; sayonara Poetry.
• Run and install command-line tools, alla npx.
• Workspaces, what?!

Installation

There are plenty of ways to get this puppy up and running in our machine. The first one, if you’re lucky enough to be on Linux or macOS:

$ curl -LsSf https://astral.sh/uv/install.sh | sh

After the installation, we have to restart our shell (just type exit in your terminal). That’s because the installer added uv to our PATH.

powershell -ExecutionPolicy ByPass -c "irm https://astral.sh/uv/install.ps1 | iex"

pip install uv

Anyways, once you’ve installed it, and as a sanity test, run:

$ uv
An extremely fast Python package manager.

Usage: uv [OPTIONS] <COMMAND>

Installing Python Versions

uv can also install and manage Python versions:

$ uv python install

That would get us the latest version, but if you want to install a specific one, just say it:

$ uv python install 3.12

To see a list of the available and installed Python versions:

$ uv python list

Projects

uv supports managing Python projects, which define their dependencies in a pyproject.toml file. Like in other languages, we can create a new Python project using the uv init command:

uv init my-proj

That will create the following project structure within the my-proj folder:

.
├── .python-version
├── README.md
├── main.py
└── pyproject.toml

The main.py file contains a simple “Hello world” program. Try it out with uv run:

$ cd my-proj
$ uv run main.py
Using CPython 3.13.2 interpreter at: /usr/bin/python3.13
Creating virtual environment at: .venv
Hello from my-proj!

Now, if we list the content of our project:

$ ls -a
.
├── .git
├── .gitignore
├── .venv
│   ├── bin
│   ├── lib
│   └── pyvenv.cfg
├── .python-version
├── README.md
├── main.py
├── pyproject.toml
└── uv.lock

That’s right, uv has created a virtual environment (in .venv folder), and initialized a git repo for us. From a project point of view, the pyproject.toml contains our project’s metadata (sort of the package.json in Node.js):

[project]
name = "hello-world"
version = "0.1.0"
description = "Add your description here"
readme = "README.md"
dependencies = []

Managing Dependencies

Managing dependencies is easy. Let’s say we want to install marimo:

uv add marimo

Marimo includes a tutorial, so let’s run it, to verify it’s installed:

uv run marimo tutorial intro

marimo tutorial
zsh: command not found: marimo

I hope that was enough to get you started; feel free to check the official docs, they’re awesome.

So you’ve been hearing about a lot of good things about Deno, want to try it out but don’t know where to start? Don’t worry, got you covered son! How about we set up a React project using the Jurassic runtime and Vite.js? This guide will also show you how to install Deno.

Installing Deno

The Deno installation in macOS/Linux, is very simple, you just need to run the following command:

curl -fsSL https://deno.land/install.sh | sh

For Windows, you can use PowerShell:

irm https://deno.land/install.ps1 | iex

Starting a new React project

To start a new React project using Deno, we’ll use Vite.js, a build tool that aims to provide a faster and leaner development experience for modern web projects. To create a new React project, run the following command:

deno run -RWE npm:create-vite-extra@latest

The npm: prefix is used to indicate that the create-vite-extra script (that will help you create a new Vite project with extra templates and options) should be fetched from the npm registry. This allows Deno to run npm packages directly without needing a separate package manager like npm or yarn.

This command will start a prompt asking you for the project name, template, and other options. Choose the React template and follow the instructions. When it finishes, you’ll see the following message:

Scaffolding project in /home/bob/react-deno...

Done. Now run:

  cd react-deno
  deno task dev

That’s it, not much to be done. Just go to the project folder and run deno task dev to start the development server. You can now start coding your new React project using Deno!

Installing packages

In the previous section we’ve seen how to create a new React project using Vite.js. Now, let’s see how to install new packages in your project. For example, let’s install React Router, a popular routing library for React:

deno add npm:react-router@latest

Formatting Code

Deno includes a built-in code formatter called deno fmt that can be used to format your code. To format all the files in your project, run the following command:

deno fmt

But running a command each time you want to format your code can be cumbersome. To make it easier, we’ll make it so that when we use a shortcut, our code is automatically formatted (it can be also be configured on save).

Installing the Deno VSCode Extension

We just have to open the Extensions panel in VSCode, and search for the Deno extension.

Initialize Workspace Configuration

Once the Deno extension has been installed, you can initialize the workspace configuration by running the Deno: Init command from the command palette (Cmd+Shift+P on macOS, Ctrl+Shift+P on Windows/Linux).

A file called .vscode/settings.json will be created in your workspace with the following configuration:

{
  "deno.enable": true,
}

That enables Deno in your workspace. Now, to configure the code formatting, we can add the following to the file above:

"[typescript]": {
    "editor.defaultFormatter": "denoland.vscode-deno"
},
"[javascript]": {
    "editor.defaultFormatter": "denoland.vscode-deno"
}

"editor.formatOnSave": true

Also, we can configure the formatting style in the deno.json file:

"fmt": {
    "options": {
      "useTabs": false,
      "lineWidth": 80,
      "indentWidth": 2,
      "singleQuote": true,
      "proseWrap": "always",
      "semiColons": false
    }
  }

This time I decided to build a landing page that closely follows zentry. Doing this project I realize that having good graphic assets can push your design quite far, with less effort.

See it live here 👈

Used Technologies

• TailwindCSS
• GSAP
• React

Another landing page, this time I decided to do an (approximate) clone of the Apple iPhone site, just to practice some GSAP animations and a bit of 3D with Three.js.

See it live here 👈

Used Technologies

• TailwindCSS
• Three.js
• React
• GSAP

Another landing page, this time about a fictitious SEO saas, powered by AI, where I tried to showcase my design and front-end skills.

See it live here 👈

Used Technologies

• TailwindCSS
• Framer-motion
• React
• Lottie files

A landing page about a fictitious Saas, where I used responsive design (mobile, tablet and desktop) in a light theme. I added some parallax effects and attractive animations.

See it live here 👈

Used Technologies

• TailwindCSS
• Framer-motion
• React